Pravděpodobnost

4.9.2016

O následující - pro mě - zajímavé věci jsem se dočetl v knize "The Joy of Knowledge: The Sciences" v českém překladu "Svět čísel, atomů a molekul" z roku 1986. V knize je na straně 41 krátký odstavec s obrázkem a též výsledkem - ovšem bez vysvětlení způsobu řešení. A mě pochopitelně zajímalo, jak se k tomuto výsledku došlo.

Zadání

Vezměme si následující úlohu. Máme tyčku (nebo třeba zápalku) délky d. Dále máme rovinu rozdělenou rovnoběžnými přímkami navzájem vzdálenými n*d. Úkolem je určit pravděpodobnost, s jakou tyčka vyhozená nad rovinou (analogie vrhu mincí) po dopadu protne libovolnou z přímek (viz obrázek).

Předpoklady

Při řešení předpokládáme, že:

Předmět, který budeme nazývat pro představu zápalka, má ideální vlastnosti - je dokonale homogenní (reálná zápalka tento předpokld pochopitelně nesplňuje).
Všechna místa v rovině mají stejnou pravděpodobnost dopadu zápalky - v takovém případě nezáleží na "velikosti" roviny ani na počtu přímek v této rovině a stačí nám spočítat pravděpodobnost protnutí přímky zápalkou pouze v jednom segmentu roviny.
Zápalka dopadne vždy buď do prostoru mezi přímkami nebo protne některou z přímek - "nekonečnost" roviny ve směru rovnoběžném s přímkami i ve směru kolmém. Při výpočtu nás tak bude zajímat pouze směr kolmý k přímkám - výpočet se tak omezí na jeden rozměr.

Zvolený způsob řešení

Výslednou pravděpodobnost určímě jako podíl počtu možností, ve kterých zápalka protne přímku a počtu všech možností dopadu zápalky. Přičemž, jak bylo zmíněno výše, počítáme pouze možnosti ve směru kolmém na přímky - v tomto směru si položíme osu x s počátkem na jedné z přímek a budeme počítat možnosti dopadu v segmentu osy x vymezeném počátkem souřadnic a následující přímkou. Délka segmentu je tedy n*d.

Počet všech dopadů

Počet všech možností dopadu zápalky v tomto segmentu je 2πnd, protože zápalka může dopadnout kdekoli na úsečce délky nd a v každém místě může být natočena v libovolném úhlu v rozmezí 0 až 2π - součinem těchto hodnot získáme již uvedený výsledek.

Počet průsečíků

Nyní spočítáme počet možností, ve kterých zápalka protne přímku. Místem dopadu budeme myslet bod, ve kterém leží střed zápalky, v takovém případě bude mít nejvzdálenější bod, ve kterém zápalka protne přímku, souřadnici rovnou d/2. Zápalka tedy protne přímku pouze v rozmezí souřadnic 0 až d/2 a (nd - d/2) až nd, nicméně nám bude stačit počítat pouze v intervalu 0 až d/2 a výsledek potom - s využitím zřejmé symetrie úlohy - vynásobíme dvěma. Nyní si pro každou hodnotu souřadnice z uvedeného intervalu určíme hodnotu úhlu natočení zápalky, při kterém se bude zápalka dotýkat přímky. Pro tento úhel platí rovnice x = d/2 cos α. Z rovnice vyjádříme úhel: α = arccos (2x/d). Toto je ve skutečnosti 1/4 úhlu, ve kterém zápalka pro dané x protne přímku - to opět plyne ze symetrie úlohy. Výsledek tedy vynásobíme čtyřmi a celkově osmi. Teď už stačí jen určit, jakým způsobem spočítáme všechny možnosti protnutí přímky. Uvážíme, že pro nekonečně malý kousek dx bude tento počet činit arccos (2x/d) dx a tedy pro interval 0 až d/2 spočítáme integrál:

$$∫↙0↖{d/2} arccos (2/d x) dx = {[}x ⋅ arccos (2/d x){]}_0^{d/2} + ∫↙0↖{d/2} x/{√{1 - 4/d^2} x^2}2/d dx =$$

$$= d/2 arccos(1) + 2∫↙0↖{d/2} x/{√{d^2 - 4x^2}} dx = 0 + ∫↙0↖{d/2} x/{√{d^2/4 - x^2}} dx =$$

$$t = d^2/4 - x^2$$

$$x = √{d^2/4 - t}$$

$$dx = 1/2 1/√{d^2/4 - t} (-1) dt$$

$$ = ∫↙{d^2/4}↖0 - √{d^2/4 - t}/√t 1/2 1/√{d^2/4 - t} dt = - 1/2 ∫↙{d^2/4}↖0 1/√t dt = -1/2 [√t 2]_{d^2/4}^0 = d/2$$

Výsledek, jak jsme řekli, vynásobíme osmi: $8 d/2 = 4d$.

Výsledek

Nyní již můžeme vypočítat pravděpodobnost: ${4d}/{2πnd} = 2/{πn}$. Pravděpodobnost, že zápalka délky d po dopadu na rovinu protne některou z rovnoběžných přímek vzájemně vzdálených nd, činí $2/{πn}$.

Testování vzorce

Abych ověřil, do jaké míry vzorec dává správnou hodnotu pravděpodobnosti, provedl jsem dva druhy pokusů. Jedna varianta spočívala v tom, že jsem si na papír nakreslil čáry a následně tisíckrát hodil zápalkou. Druhá varianta byla realizována počítačovou simulací, kdy poloha dopadlé zápalky byla náhodně generována ve dvaceti tisících případech. Obě varianty jsem testoval se dvěmi sadami parametrů: 1) d = 3 cm, n = 4/3 a 2) d = 1 cm a n = 4. Získané výsledky jsem vynesl do grafů, ve kterých je vidět závislost četnosti protnutí přímky zápalkou na počtu pokusů.

Hody zápalkou - 1000 pokusů pro hodnoty d = 3 cm a n = 4/3

Výsledná četnost z pokusu vychází 49.7 %. Výpočet podle vzorce dává hodnotu pravděpodobnosti 47.75 %.

Hody zápalkou - 1000 pokusů pro hodnoty d = 1 cm a n = 4

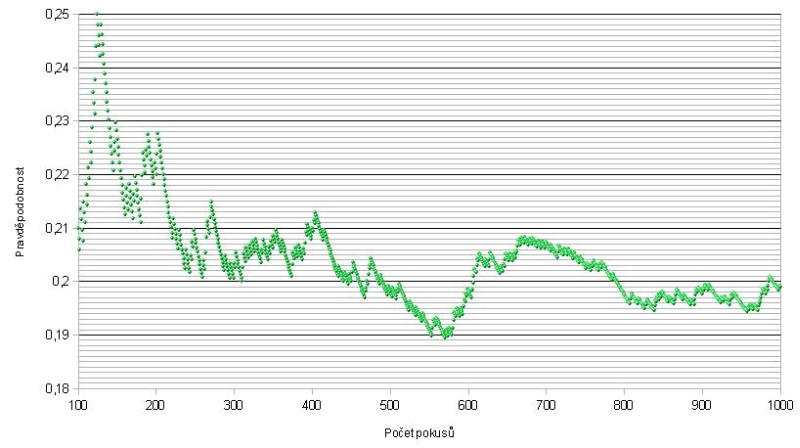
Výsledná četnost z pokusu vychází 19.9 %. Výpočet podle vzorce dává hodnotu pravděpodobnosti 15.92 %.

Počítačová simulace - 20000 pokusů pro hodnoty d = 3 cm a n = 4/3.

Výsledná četnost z pokusu vychází 47.58 %. Výpočet podle vzorce dává hodnotu pravděpodobnosti 47.75 %.

Počítačová simulace - 20000 pokusů pro hodnoty d = 1 cm a n = 4.

Výsledná četnost z pokusu vychází 15.58 %. Výpočet podle vzorce dává hodnotu pravděpodobnosti 15.92 %.