MATEMATIKA ELEKTRONIKA POČÍTAČE HRY OSOBNÍ KONTAKT

ZÁKLADNÍ POJMYVĚTY, POUČKY, ZAJÍMAVOSTIÚLOHYPŘIJÍMACÍ ZKOUŠKY NA VŠMATURITNÍ ZKOUŠKAPŘIJÍMACÍ ZKOUŠKY NA SŠNÁSTROJEZÁKLADNÍ ŠKOLADOUČOVÁNÍPřidat úlohu

Přijímací zkouška z matematiky na VŠ - rok 2018

16.1.2019

V tomto textu projdu zadání z matematiky u přijímaček na Matematicko-fyzikální fakultu Univerzity Karlovy z roku 2018, přičemž se pokusím relativně podrobně popsat řešení jednotlivých úloh.

Fakulta tato zadání zveřejňuje na stránkách pro uchazeče o studium. Zadání je k dispozici ve formě PDF souboru - netuším ovšem, jak je to s autorskými právy. Proto zde zadání nebudu uvádět a pouze poskytnu webový odkaz na dané PDFko: zadání pro rok 2018 je zde.

Zadání jsou ve formě testů, kdy ke každé úloze je 5 otázek, na které lze odpovědět ANO či NE. Je možné více správných odpovědí. Poskytované zadání obsahuje pouze správné odpovědi na otázky, ale už ne popis řešení. Jsou dvě varianty testů A a B - na úlohu se budu vždy odkazovat písmenem varianty a číslem úlohy - např. A1.

Řešení úloh: A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 B1 B2 B3 B4 B5 B6 B7 B8 B9 B10

Úloha A1

Zadaná funkce obsahuje absolutní hodnotu, funkci si tedy zapíšu ve vhodnějším tvaru:

Všechny vlastnosti funkce snadno určím, pokud si načrtnu její graf. Pro kladná $x$ je to klasická parabola a pro záporná je to parabola "otočená dolu". V nule má hodnotu 0.

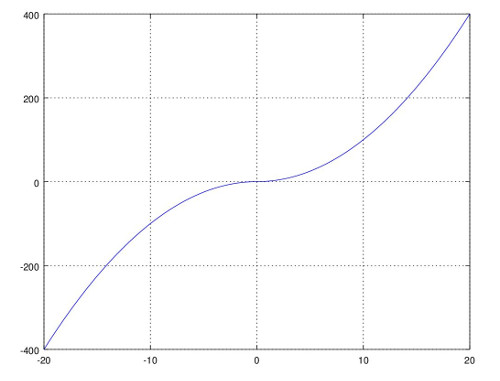
Funkce není sudá, protože $f(-x)≠f(x)$. Funkce je lichá, protože $f(-x)=-f(x)$, což přímo plyne z přepisu funkce nahoře. Funkce není periodická, protože neexistuje takové reálné číslo $k$ různé od nuly, aby platilo $f(x)=f(x+k)$. Funkce je rostoucí, což můžu ukázat například tak, že první derivace funkce je kladná pro všechna $x$ (kromě nuly):

A konečně funkce je prostá - můžu to ukázat na základě definice, která říká, že funkce je prostá tehdy, když pro žádné dvě různé hodnoty $x_1$, $x_2$ z definičního oboru neplatí $f(x_1)=f(x_2)$. To, že je funkce prostá, také můžu určit z toho, že je rostoucí.

Úloha A2

Při pohledu na rovnici je zřejmé, že pro $x$ musí platit $x≠2$ a $x≠-2$, protože oba jmenovatele musí být různé od nuly. Rovnici upravujeme:

Aby byl součin na levé straně roven nule, musí platit $x=0$ a/nebo $2k+1=0$. Zkombinováním těchto podmínek společně s podmínkami, které jsme stanovili úplně na počátku, dojdeme k závěru, že pro $k=-1/2$ jsou řešením rovnice všechna reálná čísla kromě {$-2$;$2$}. Pro $k≠-1/2$ je řešením $x=0$.

Úloha A3

První čtverec má stranu délky $d_1=a$, obvod $o_1=4a$ a obsah $S_1=a^2$. Délku strany druhého čtverce určíme pomocí Pythagorovy věty:

Obecně délku strany $i$-tého čtverce určíme z předchozí délky:

To znamená, že délky stran čtverců tvoří geometrickou posloupnost. Každá další strana je ${√2}/2$ krát delší než předchozí. Z toho taktéž plyne, že i obvody a obsahy budou tvořit geometrickou posloupnost:

Nyní jsme připraveni odpovídat na testové otázky. Jelikož kvocient geometrické posloupnosti obsahů čtverců $1/2$ je menší než $1$, bude součet obsahů všech čtverců konečný. Tento součet snadno spočítáme podle vzorce pro součet geometrické řady:

Podobně spočítáme součet obvodů, protože ${√2}/2<1$:

Obvod čtvrtého čtverce není jednou čtvrtinou obvodu druhého čtverce, protože ${o_4}/{o_2}={q_o}^2={({√2}/2)}^2=1/2≠1/4$. Obsah pátého čtverce je jednou polovinou obsahu čtvrtého čtverce, protože ${s_5}/{s_4}=q_s=1/2$.

Úloha A4

Vzhledem k tomu, že se v rovnici proměnná $x$ nachází pod druhou odmocninou, je zřejmé, že musí být $x≥0$. Upravujeme rovnici umocněním obou stran na druhou:

Získali jsme řešení rovnice $x=\{45°;135°\}+360°k$, $k∈\{0;N\}$. První tvrzení je neplatné, protože řešení vyhovují pouze $x≥0$. Druhé tvrzení je taktéž neplatné, protože např. hodnota 45°+π=45°+180°=225° nevyhovuje rovnici.Třetí tvrzení je platné, protože $2π$ je perioda funkce sinus. Aby bylo pravdivé čtvrté tvrzení, muselo by platit, že dvojnásobek řešení má totožný tvar jako řešení samotné, což není pravda:

Podobně se podíváme na páté tvrzení:

Toto tvrzení je tedy platné, protože odvozený vztah odpovídá tvaru řešení.

Úloha A5

Budeme upravovat výraz na pravé straně:

A to je vlastně vše, protože rozhodnout o platnosti tvrzení je triviální záležitost.

Úloha A6

U této úlohy je vhodné si načrtnout obrázek, ze kterého budou patrné přibližné hodnoty souřadnic hledaných bodů a taktéž bude snadné ověřit podmínku o značení vrcholů proti směru pohybu hodinových ručiček.

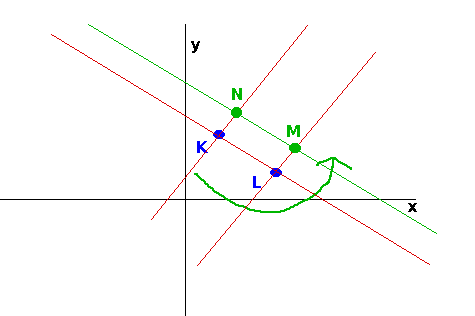
Při řešení budu postupovat tak, že nejprve určím vektor $u↖{→}=L-K=(4;-3)$. K němu najdu nějaký kolmý vektor, například $n↖{→}=(3;4)$, ovšem potřebuju, aby měl třetinovou velikost vektoru $u↖{→}$. Takže ho upravím $v↖{→}=1/3n↖{→}=(1;4/3)$ - vektor $v↖{→}$ má nyní jak velikost strany $LM$, tak i její směr, resp. míří od $L$ k $M$. Souřadnice bodu $M$ tedy získám tak, že k bodu $L$ tento vektor přičtu: $M=L+v↖{→}=[7;10/3]$. Souřadnice bodu $N$ získám přičtením stejného vektoru k bodu $K$: $N=K+v↖{→}=[3;19/3]$. Vzdálenost $|LM|$ je rovna velikosti vektoru $v↖{→}$: $|LM|=|v↖{→}|=√{1+16/9}=5/3$. Obsah obdélníku KLMN se spočítá jako součin $|KL|*|LM|=3*|LM|*|LM|=3*{5/3}*{5/3}=25/3$.

Úloha A7

Délka $|AB|$ se vypočítá užitím Pythagorovy věty (úhel $BAG$ je pravý):

Obvod útvaru $ABCDEFG$ je $o=20√2+60$ cm. Obsah trojúhelníku $ABG$ je $S_{ABG}=1/2{|AB|}^2=100$ ${cm}^2$. Obsah útvaru $ABCDEFG$ je $S=S_{ABG}+|CD|*|DE|=100+200=300$ ${cm}^2$. Vzdálenost $|AF|$ se opět spočte užitím Pythagorovy věty:

Úloha A8

Číslo nebude začínat nulou, takže na první pozici vybíráme z pěti číslic. Na druhou pozici taktéž z pěti číslic, na třetí ze čtyř a na čtvrtou ze tří. Celkem je to $X=5*5*4*3=300$ možností.

Čtyřciferné sudé číslo tvořené z nabízených číslic bude končit některou číslicí z množiny $\{0,2,4,6\}$. Počet čísel končících $0$ bude $Y_0=5*4*3=60$ - na posledním místě je nula, na třetí místo vybírám z $5$ti číslic, na druhé místo ze $4$ číslic a na první místo ze $3$. Počet čísel končících $2$ bude $Y_2=5*4*3-4*3=60-12=48$ - na posledním místě je dvojka a dále první část v součtu stejná jako v předchozím případě. Liší se to, že musím odečíst případy, kdy jsem na první místo zvolil nulu, která tam nepatří. Těchto "omylů" je $4*3=12$, protože na posledním místě je dvojka, na prvním místě je nula a na třetí pozici tak vybírám ze $4$ číslic a na druhou pozici ze $3$ číslic (nebo obráceně, na tom nesejde). Stejné počty jsou i v případě $4$ky a $6$ky na posledním místě a platí tedy $Y_4=Y_6=Y_2$. Celkový počet sudých čtyřciferných čísel tvořených nabízenými číslicemi je celkem $Y=Y_0+Y_2+Y_4+Y_6=60+3*48=204$.

Úloha A9

Pokud vyraz v závorce umocním na desátou, ve výsledném polynomu bude nejvyšší mocnina u $x$ $20$, protože ${(x^2)}^10=x^20$ neboli stupeň mnohočlenu bude $20$ - tolik k prvním dvěma tvrzením. K určení kořenů výsledného polynomu nám stačí určit kořeny výrazu $(1+2x-x^2)$:

A tedy výsledný polynom stupně $20$ má celkem deset těchto dvojic kořenů. Kořeny $1-√2$ jsou záporné. Ani jeden kořen není celočíselný, protože $√2$ je iracionální číslo. Součet každých dvou různých kořenů je kladný, protože $(1-√2)+(1+√2)=2>0$.

Úloha A10

Znázorním si hody kostkou, kdy nedojde k ukončení hry, to znamená, kdy je součet bodů menší než $4$. Na prvním řádku budou varianty po prvním hodu, na druhém řádku po druhém hodu atd.

     1      2      3
    / \    /
   1  2   1
  /
 1

V každém dalším hodu, který není znázorněný, hra končí, protože součet bude větší než $3$. Z toho plyne, že hra skončí nejpozději po čtvrtém hodu. Začnu třetím tvrzením - hra zcela jistě skončí součtem menším než $10$. Je to zřejmé ze znázorněného grafu - pokud přičtu nejvyšší možnou variantu hodu $6$ bodů ke kterémukoli součtu v grafu, dostanu vždy číslo $9$.

Pravděpodobnost, že hra skončí po prvním hodu, je $1/2$, protože z celkových šesti možností $\{1,2,3,4,5,6\}$ ve třech z nich $\{4,5,6\}$ hra končí a tedy $p_1=3/6=1/2$.

Pravděpodobnost, že hra skončí po druhém hodu, je $5/12$, protože pravděpodobnost, že k druhému hodu vůbec dojde, je $1/2$, celkový počet variant je $3*6=18$ a z toho v $15$ti případech hra končí. Takže $p_2={1/2}*{15/18}=5/12$. Čtvrté tvrzení je tedy pravdivé, protože $5/12≥1/3$.

Pravděpodobnost, že hra skončí po více než dvou hodech je identická s pravděpodobností, že hra skončí po třetím nebo čtvrtém hodu, protože pravděpodobnost, že hra skončí po více než čtyřech hodech je $0$. Po třetím hodu hra skončí s pravděpodobností $p_3={1/2}*{3/18}*{17/18}=17/216$. Po čtvrtém hodu hra skončí s pravděpodobností $p_4={1/2}*{3/18}*{1/18}*1=1/216$. Tím pádem pravděpodobnost, že hra skončí po více než dvou hodech, je $p_{34}=p_3+p_4={17/216}+{1/216}=1/12<1/3$ a tudíž páté tvrzení není pravdivé. Tuto pravděpodobnost jsme též mohli určit jednodušeji jako $p_{34}=1-(p_1+p_2)=1-1/2-5/12=1/12$.

Pro zodpovězení první a druhé otázky se podíváme na to, jakými způsoby je možné dosáhnout konečných součtů $5,6,7$. Když hra skončí po prvním hodu, tak jsou zde hodnoty $5,6$ zastoupeny ve stejném počtu, ale $7$ pochopitelně chybí. Ve všech dalších případech, je zastoupení součtů $5,6,7$ stejné, protože vždy přičítám k číslu $3$ a k uvedeným součtům vede vždy jen jedna varianta: $5=3+2, 6=3+3, 7=3+4$. Celkově vzato pravděpodobnost, že hra skončí součtem $5$ je stejná jako pravděpodobnost, že skončí součtem $6$. Naopak pravděpodobnost, že hra skončí součtem $7$ je menší právě proto, že sedmička chybí v množině čísel po konci při prvním hodu. Tedy první tvrzení pravdivé není (platí $p_5=p_6$), kdežto druhé tvrzení pravdivé je (platí $p_6>p_7$).

Úloha B1

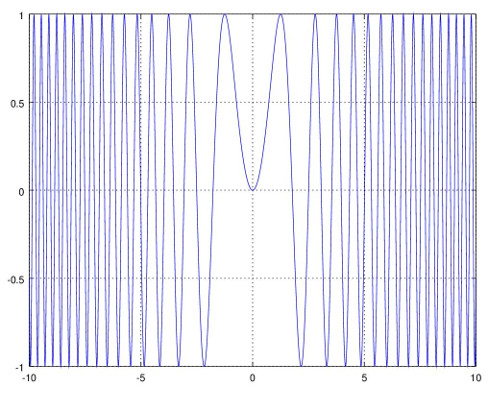
Jelikož platí $f(-x)=sin({(-x)}^2)=sin(x^2)=f(x)$, funkce je sudá a tudíž není lichá. Funkce není periodická, protože "perioda" funkce sinus se kontinuálně zmenšuje, jak ukazuje graf funkce. Funkce není rostoucí, protože její první derivace $f'(x)=2xcos(x^2)$ osciluje mezi zápornými a kladnými hodnotami. Funkce není prostá, protože například pro $x_1=0°$ a $x_2=6{√5}°$ platí $f(x_1)=f(x_2)=0$.

Úloha B2

Na první pohled je zřejmé, že parametr $p$ nemůže být roven nule. Upravujeme rovnici:

Chceme rovnici vydělit výrazem v závorce na levé straně. V tom případě, ale musí být tento výraz různý od nuly. Pokud ovšem bude rovný nule, tak:

Pokud dosadíme $p=2$ do (1), zjistíme, že rovnice nemá řešení. Naopak pro $p=-2$ má rovnice nekonečně mnoho řešení (matematicky řečeno řešením rovnice jsou všechna reálná čísla). V případě, že $p≠±2$, tak:

Závěr tedy zní, že pro $p=0$ nebo $p=2$ nemá rovnice řešení. Pro $p=-2$ má rovnice nekonečně mnoho řešení. Pro $p≠0$ a $p≠±2$ má rovnice řešení $x=1/{p(p-2)}$.

Úloha B3

První trojúhelník má délku strany $d_1=a$, obvod $o_1=3a$ a obsah $S_1={{√3}/4}a^2$. Hodnoty pro každý další trojúhelník se spočítají z hodnot předchozího trojúhelníku:

Zjistili jsme, že délky stran a obvody trojúhelníků tvoří geometrické posloupnosti s kvocientem v obou případech ${√3}/2$ a obsahy trojúhelníků tvoří geometrickou posloupnost s kvocientem $3/4$. Součet obsahů všech trojúhelníků bude konečný, protože kvocient geometrické posloupnosti $q_S=3/4<1$. Ze vzorce pro součet geometrické řady spočítáme:

Třetí tvrzení je pravdivé, protože $o_n={q_o}^2o_{n-2}={3/4}o_{n-2}$. Páté tvrzení není pravdivé, protože $o_5={q_o}^4o_1={9/16}o_1≠{1/2}o_1$.

Úloha B4

Logaritmická funkce je definována pouze pro kladné hodnoty, stanovíme tedy podmínky, za kterých je rovnice řešitelná:

Za uvedených podmínek řešíme rovnici:

Pravdivá jsou tedy pouze tvrzení číslo 3 a 5. První je zřejmé, druhé vyplývá z tohoto:

Úloha B5

Zavedeme substituci a řešíme soustavu:

Zjistíme, že vyhovují $a=2$, $b=32$, neboli:

Řešením tedy je $x=3$ a $y=2$.

Úloha B6

Určíme souřadnice bodu $C$: $C=2S-A=[8;3]$. Vezmeme vektor kolmý k úhlopříčce $AS$ o stejné velikosti a přičteme/odečteme ho od bodu $S$ - tím získáme vrcholy $B$, $D$: $u↖{→}=S-A=(2;1)$, $n↖{→}=(1;-2)$. Je potřeba dát pozor, abychom vrcholy správně označili s ohledem na požadavek značení proti směru pohybu hodinových ručiček. Bude tedy $B=S+n↖{→}=[7;0]$ a $D=S-n↖{→}=[5;4]$. Velikost $|BD|=2|u↖{→}|=2|n↖{→}|=2√5$. Obsah čtverce je $S={|BC|}^2=10$.

Úloha B7

Čtverec má stranu $a=√S=√{16}=4$. Označme $v$ výšku trojúhelníku $ABK$, pak $v=4*sin60°=4{{√3}/2}=2√3$. Vzdálenost $|KM|=2v+a=4√3+4=4(1+√3)$. Vzdálenost $|KL|=√{2{(v+a/2)}^2}=√2(2+2√3)=2(√2+√6)$. Obsah čtverce $KLMN$ je $S=4(2+6+2√{12})=16(2+√3)$. Obvod čtverce $KLMN$ je $o=8(√2+√6)$. Vzdálenost $|KD|=√{4+{(4+2√3)}^2}=√{32+8√{12}}=4√{2+√3}$.

Úloha B8

Číslo je dělitelné $4$ tehdy, jestliže je jeho poslední dvojčíslí dělitelné $4$. Z nabízených číslic $\{1;5;6;8;9\}$ je možné sestavit pět takových dvouciferných čísel: $16$, $56$, $68$, $88$, $96$. Čtyřciferných čísel dělitelných čtyřmi sestavených z uvedených číslic je celkem $Z=5*5*5=125$, protože na třetí a čtvrtou pozici vybírám z pěti možností, na druhou pozici vybírám z pěti možností a na první pozici taktéž. Čtyřciferných čísel splňujících dané podmínky navíc s požadavkem, že se číslice nesmějí opakovat, je $T=4*3*2=24$, protože počet dvouciferných čísel dělitelných čtyřmi se snížil na $4$ (číslo $88$ nevyhovuje dodatečné podmínce), tudíž na třetí a čtvrtou pozici vybírám ze čtyř možností, na druhou pozici ze tří možností a na první pozici ze dvou možností.

Úloha B9

Výraz má smysl pouze pro $x≠5$. Za této podmínky mnohočleny ve zlomku vydělíme a získáme tak:

Aby byl výraz celým číslem, musí být celým číslem zlomek $11/{x-5}$. Protože $11$ je prvočíslo, musí být $x-5$ rovno buď $±1$ nebo $±11$. Z těchto podmínek získáme $x∈\{-6;4;6;16\}$.

Úloha B10

Můžeme uvažovat třeba tak, že na začátku máme $10$ nul v řadě a na místo některých z nich budeme rozmísťovat $6$ jedniček. Takových možností je celkem $|M|=(\table \10 ; \6)={7*8*9*10}/{2*3*4}=210$.

Třetí tvrzení je nepravdivé. Počet posloupností začínajících $0$ je $P_0=(\table \9 ; \6)={7*8*9}/{2*3}=84$, protože na první pozici je $0$, rozmísťuju $6$ jedniček na $9$ pozic. Počet posloupností začínajících $1$ je $P_1=(\table \9 ; \5)={6*7*8*9}/{2*3*4}=126$, protože na první pozici je $1$, rozmísťuju $5$ jedniček na $9$ pozic. Je zřejmé, že $P_0≠P_1$.

Čtvrté tvrzení je pravdivé. Jsou $4$ možnosti, jak můžou vypadat dvě poslední pozice: $00$, $01$, $10$, $11$. Pokud se ovšem posloupnost $8$mi předchozích číslic má lišit, musím jednu z dvojice $01$ a $10$ vynechat. Mám tedy $3$ možnosti $00$, $01$, $11$. V prvním případě první až osmou pozici můžu obsadit $P_{x00}=(\table \8 ; \6)=28$mi způsoby. Druhý případ $P_{x01}=(\table \8 ; \5)=56$. Třetí případ $P_{x11}=(\table \8 ; \4)=70$. Celkem je to $P=P_{x00}+P_{x01}+P_{x11}=28+56+70=154$ posloupností.

Páté tvrzení je pravdivé. Na začátku posloupnosti je $1$ jednička a $3$ nuly, které můžu rozmístit $(\table \4 ; \1)=4$mi způsoby. Na zbytek posloupnosti mi zbývá $5$ jedniček a $1$ nula, které můžu rozmístit $(\table \6 ; \5)=6$ti způsoby. Celkový počet takovýchto posloupností tedy je $4*6=24$.