ZÁKLADNÍ POJMYVĚTY, POUČKY, ZAJÍMAVOSTIÚLOHYPŘIJÍMACÍ ZKOUŠKY NA VŠMATURITNÍ ZKOUŠKAPŘIJÍMACÍ ZKOUŠKY NA SŠNÁSTROJEZÁKLADNÍ ŠKOLADOUČOVÁNÍPřidat úlohuPřidat řešení úlohyPřidat komentář
Stín
Ladislav Veiner, 08.08.2018 11:02
Představme si okno na zdi domu, ze kterého se díváme směrem ke slunci. Otázka zní, v jaké maximální výšce nad zemí musí letět pták (velikosti řekněme třeba kosa), aby v daný okamžik svým tělem zakryl celé slunce. Úlohu řešte s následujícími údaji a podmínkami.
Dům stojí na rovině a zeď s oknem je k zemi kolmá (rovina okna prochází středem Země). Okno má rozměry (šířka x výška) 250 cm x 150 cm, a nachází se ve výšce 4 metry nad zemí. Naši dvojici očí sledujících slunce nahradíme bodem ležícím ve středu okna. Dům s oknem leží na severní polokouli 70 ° od rovníku. Je právě letní období - tedy část roku, kdy je severní zemský pól "přikloněný" ke Slunci - a zároveň je pravé poledne. Pro zjednodušení považujte Zemi za dokonalou kouli o poloměru 6370 km. Rovina zemského rovníku svírá s oběžnou dráhou úhel 23.5 °. Slunce berte jako dokonalou kouli o poloměru 695700 km ve vzdálenosti 150 milionů kilometrů od středu Země. Tvar ptáka považujte (s oběma očima zavřenýma :-)) za kouli o průměru 30 cm. Fyzikální aspekty šíření světla zjednodušíme na tvrzení, že světlo se šíří všemi směry od zdroje rovnoměrně a přímočaře.
Přidat řešení úlohy Přidat komentář
Řešení číslo 1, Ladislav Veiner, 21.08.2018 13:28
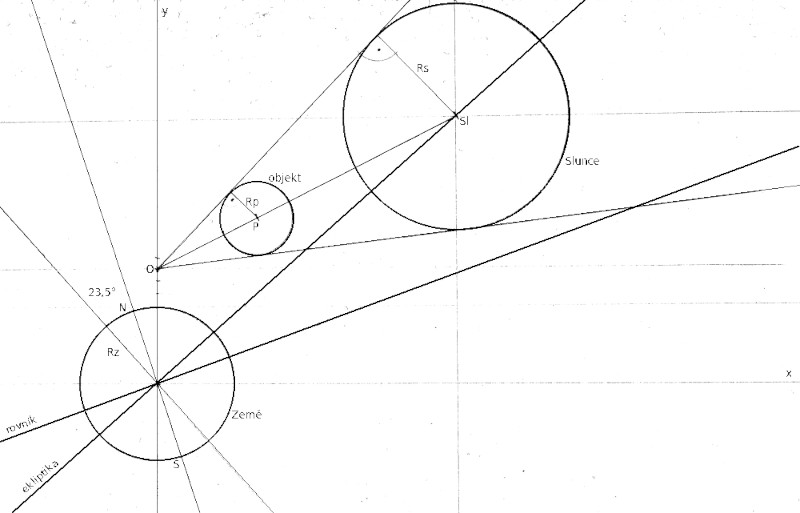
Na obrázku dole je zachycena situace (poměry vzdáleností neodpovídají skutečnosti - obrázek má za úkol názorně ukázat geometrii úlohy). Naznačená souřadná soustava je zvolena tak, že počátek leží ve středu Země a rovina $XY$ prochází pozorovacím místem a středem Slunce. Z-ovou osu nemusíme uvažovat, protože pro řešení nám stačí 2 rozměry. Značení na obrázku: $N$ - zemský severní pól, $S$ - jižní pól, $Rz$ - poloměr Země, $Rs$ - poloměr Slunce, $Rp$ - poloměr stínícího objektu, $Sl$ - poloha středu Slunce, $P$ - poloha středu objektu, $O$ - pozorovací místo (střed okna).
Přímka na obrázku označená "ekliptika" a procházející středy Země a Slunce je průmětem dráhy Země okolo Slunce. Přímka, která je od ní odchýlená o $23.5°$ představuje průmět světového rovníku. Kolmo k němu je zemská rotační osa, která Zemi protíná v bodech $N$ a $S$. Pozorovací místo leží na 70. stupni severní šířky a tedy přímka procházející tímto místem a středem Země - v obrázku shodná s y-ovou osou - svírá s rovníkem úhel $70°$.
To, že nějaký objekt zcela zakryje slunce, geometricky znamená, že se jednak objekt nachází mezi námi a Sluncem a také, že každá polopřímka vedená z našeho oka do libovolného bodu slunce prochází tímto objektem. Největší vzdálenost, ve které se může objekt dané velikosti nacházet, aby zcela zakryl slunce, je dána podmínkou (jak je vidět na obrázku), že polopřímka vycházející z oka, která je ve 2D zobrazení tečnou kružnice zobrazující Slunce, je zároveň tečnou kružnice objektu (a naopak). Je zřejmé, že pokud by byl objekt dále, nezakryje celé slunce, a pokud by byl blíže, zakryje slunce vždy, když se střed objektu bude "nacházet poblíž" spojnice oka a středu slunce).
K tomu, abychom určili výšku objektu nad zemí, potřebujeme znát vzdálenost objektu od oka $|OP|$. Tu určíme pomocí podobných trojúhelníků, kdy platí:
$${Rp}/{|OP|}={Rs}/{|OSl|}$$
Vzdálenost oka a středu Slunce $|OSl|$ můžeme vypočítat tak, že určíme x-ovou a y-ovou složku vzdálenosti Země-Slunce $|ZSl|$ a následným užitím Pythagorovy věty. Úhel, který svírá spojinice Země-Slunce a y-ová osa, je roven $70°-23.5°=46.5°$.
$$|ZSlx|=|ZSl|sin(46.5°)$$
$$|ZSly|=|ZSl|cos(46.5°)$$
$$|OSl|^2=|ZSlx|^2+(|ZSly|-Rz-4-0.75)^2$$
V posledním vztahu hodnota $4$ reprezentuje výšku okna nad zemí v metrech a $0.75$ polovinu výšky okna taktéž v metrech. Ještě zbývá zjistit, jak ze vzdálenosti $|OP|$ určit výšku nad zemí. Spočítáme, čemu se rovná úhel, který svírá spojnice okno-Slunce a x-ová osa. Tento úhel označíme třeba $o$:
$$sin(o)={|ZSly|-Rz-4-0.75}/{|OSl|}$$
Potom se bude výška objektu nad zemí - označme třeba $H$ - rovnat:
$$H={|OP|}sin(o)+4+0.75$$
Dosadíme již odvozené vztahy a následně hodnoty vzdáleností v metrech:
$$H={|OP|}sin(o)+4.75={|OSl|}{{Rp}/{Rs}}{|ZSly|-Rz-4-0.75}/{|OSl|}+4.75=$$
$$={{Rp}/{Rs}}(|ZSly|-Rz-4.75)+4.75={{Rp}/{Rs}}(|ZSl|cos(46.5°)-Rz-4.75)+4.75$$
$$H={0.15/{6957*10^5}}(15*10^10*cos(46.5°)-6370*10^3-4.75)+4.75 m=27.01 m$$
Odpověď zní, že kos by musel letět maximálně ve výšce přibližně 27 metrů nad zemí.