
ZÁKLADNÍ POJMYVĚTY, POUČKY, ZAJÍMAVOSTIÚLOHYPŘIJÍMACÍ ZKOUŠKY NA VŠMATURITNÍ ZKOUŠKAPŘIJÍMACÍ ZKOUŠKY NA SŠNÁSTROJEZÁKLADNÍ ŠKOLADOUČOVÁNÍPřidat úlohuPřidat řešení úlohyPřidat komentář
Laser
Ladislav Veiner, 25.11.2018 13:05
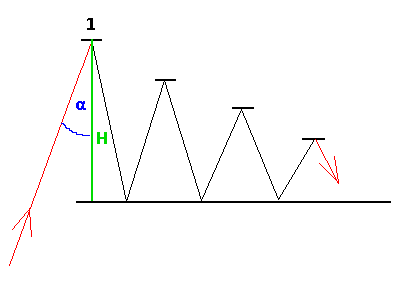
Představme si, že máme zdroj laserového paprsku, který svítí určitým směrem. V cestě tomuto paprsku leží rovinné zrcátko (na obrázku dole označené jako 1), na které paprsek dopadne pod úhlem 30° (kolmice k zrcátku a paprsek svírají tento úhel), který označíme α. Od zrcátka se paprsek odrazí a pokračuje k velkému rovinnému zrcadlu, které je rovnoběžné s malým zrcátkem číslo 1. Dále paprsek směřuje ke zrcátku číslo 2 a opět se odráží k velkému zrcadlu. Celá situace ja načrtnuta na obrázku. Malá zrcátka jsou postupně stále blíže k velkému zrcadlu, až poslední "zrcátko" splyne s velkým zrcadlem a místo odrazu paprsek pohltí.
Jako obvykle řešíme matematickou nikoli fyzikální úlohu. Paprsek považujeme za ideální, jeho intenzita se nemění ("doletí jakkoli daleko"), pohybuje se po přímé dráze, při odrazu je úhel dopadu roven úhlu odrazu, paprsek je "nekonečně úzký" neboli jeho dráhu považujeme za přímku.
Známe tyto údaje:
Vzdálenost prvního zrcátka od velkého zrcadla je H=3.25 m.
Paprsek dopadne na první zrcátko pod úhlem α=30°.
Absolutní hodnota rozdílu vzdáleností dvou po sobě následujících zrcátek od velkého zrcadla je konstantní a je rovna 5H-16.
Úkolem je určit, jak velkou vzdálenost od prvního zrcátka (měřeno podél velkého zrcadla) paprsek urazí, než bude pohlcen (posledním pseudozrcátkem). Jinak řečeno, v jaké vzdálenosti od prvního zrcátka se nachází poslední zrcátko?
Přidat řešení úlohy Přidat komentář
Řešení číslo 1, Ladislav Veiner, 02.12.2018 23:11
Pro určení vzdálenosti, kterou paprsek uletí, potřebujeme vědět, kolik zrcátek je na celé trase. Jelikož vzdálenost zrcátek od velkého zrcadla se zmenšuje o konstantu, tvoří tyto hodnoty aritmetickou posloupnost. První člen je roven $H=3.25$ a absolutní hodnota diference je $5H-16=5*3.25-16=0.25$. Protože je posloupnost klesající, bude diference záporná $-0.25$. Pro vzdálenost $i$-tého zrcátka platí:
$$h_i=3.25-0.25*(i-1)$$
Víme, že poslední zrcátko splývá s velkým zrcadlem - to znamená, že jeho vzdálenost je rovna nule:
$$0=3.25-0.25*(i-1)$$
$$i={3.25}/{0.25}+1$$
$$i=14$$
Na trase je tedy celkem 14 zrcátek.
Celkovou vzdálenost v horizontálním směru rozdělíme na dvě části. První bude tvořit cesta od prvního zrcátka do místa prvního odrazu od velkého zrcadla. Druhou částí bude zbytek trasy.
Jelikož známe úhel $α=30°$, tak je první část vzdálenosti rovna:
$$x_1=H*tgα=3.25*tg30°=3.25{1/{√3}}=3.25/{√3}$$
Druhá část se skládá z úseků, kdy paprsek letí od místa odrazu na velkém zrcadle k malému zrcátku a znovu směrem k místu dalšího odrazu od velkého zrcadla. Těchto dílčích úseků je 12. První úsek je dlouhý:
$$2*(tg30°)*(H-0.25)=6/{√3}$$
K-tý úsek je dlouhý:
$$2*(tg30°)*(H-k*0.25)=2*{1/{√3}}*3.25-2*{1/{√3}}*0.25*k=6.5/{√3}-{0.5/{√3}}k$$
Poslední úsek (vezmu předchozí vztah a za $k$ dosadím $12$):
$$6.5/{√3}-{0.5/{√3}}12=0.5/{√3}$$
Tyto úseky tvoří aritmetickou posloupnost s diferencí $-{0.5/{√3}}$. Součet této posloupnosti je roven délce druhé části celé trasy. A tedy (použiju vzorec pro součet členů aritmetické posloupnosti, což je aritmetický průměr prvního a posledního prvku násobený počtem prvků):
$$x_2=12{{6/{√3}+0.5/{√3}}/2}=39/{√3}$$
Délka celé trasy v horizontálním směru je součtem délek obou částí:
$$x_1+x_2=3.25/{√3}+39/{√3}=42.25/{√3}=24.39$$
Výsledkem úlohy je odpověď, že paprsek v horizontálním směru urazí přibližně $24.39$ metrů.
Přečtěte si více o součtu aritmetické posloupnosti.